Jarduera A
Jarduera hau bi eratara egin daiteke, bai eskuz bai Geogebraren bidez, baina aukeratzen duzuena aukeratzen duzuela, guztiz beharrezkoa da matematika-ezagutza batzuk izatea .
Ondo pentsatu zer egiten duzuen eta ea aurkezten dizuegun arazoa konpontzen laguntzen diguzuen!
Euskal baserri bat eraikitzeko asmoa dugu, baina diruz eskas gabiltza lan hori burutzeko. Argi dugu baserri horrek ezinbesteko ezaugarri batzuk izan behar dituela:

— Laukizuzen itxurazko oinarria, luzera zabaleraren bikoitza izanik.
— Egitura nagusiaren bolumena 972 m3-koa izango da.
— Teilen prezioa erosiko dugun kantitatearen araberakoa da, honako funtzio honi jarraikiz:
p(x) = x – 400. Teila guztien kostua ahalik eta txikiena izatea nahi dugu.
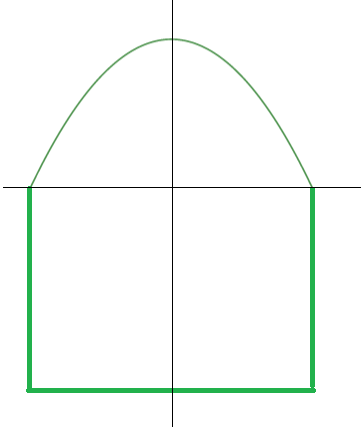
— Atearen azaleraz hau dakigu: laukizuzen itxurakoa da eta goiko zatia y=1-x2 funtzioak adierazten du, x=-1, x=1 eta y=-2 zuzenek laukizuzena eratzen dutelarik.
Aurrekontua errespetatzeko, hormak eta sabaia margotzeko erabiliko dugun materialaren kostua ahalik eta txikiena izatea nahi bada, zein izango dira gure baserriaren dimentsioak?
Zenbat teila erosi behar ditugu kostua minimizatzeko?
Zenbat metro karratu neurtzen ditu ateak? Atearen lodiera 5 zentimetrokoa bada, zenbat metro kubiko egur beharko dugu?
Jarduera B
Haize-errota bat eraiki nahi dugu. Honako ezaugarriak bete behar ditu:
–Zilindro batez eta kono batez eratuta egongo da. Zilindroaren bolumena 125 Π metro kubikokoa izango da eta, harritxoz estaliko dugunez, alboko eta lurreko azalerak ahalik eta txikienak izatea nahi dugu.
–Konoaren erradioazilindroaren berdina izango da, eta altuera, berriz, zilindroaren altueraren erdia.
Aurkitu zenbat neurtu behar duten erradioak eta altuerak aukeratu ditugun baldintzak betetzeko.
Bestalde, errotaren hegalek biraka dabiltzanean egiten duten distantzia, denboraren menpeko funtzio honek ematen digu: s(t) = 0.4t + 3. Kalkulatu hegalen abiadura lineala.